Histogramas, datos continuos y el medallista misterioso
Histogramas, datos continuos y el medallista misterioso

En los Juegos Olímpicos de París año 1900, el equipo holandés de Remo decidió sustituir a su timonel en la final. En su lugar, reclutaron a un niño desconocido de entre 7 y 10 años. La ventaja de peso resultó decisiva y ganaron el oro por menos de un metro en la línea de meta.
Más de un siglo después, aquel niño sigue siendo un misterio y se desconoce su identidad e incluso nacionalidad. Ganó la carrera, se hizo la foto de campeones y se esfumó entre el público. Todo apunta a que aquel niño es el campeón olímpico más joven de la historia, aunque no tengamos datos para confirmarlo.
Si deseas analizar la edad de los campeones olímpicos gráficamente, podrías considerar utilizar un histograma. Un histograma es una herramienta gráfica que se utiliza para representar la distribución de frecuencias de un conjunto de datos. En este caso, podrías representar la distribución de edades de los campeones olímpicos en un histograma para analizarla visualmente. El motivo es que la edad de una persona es lo que en matemáticas llamamos una variable continua. Para ellas, es mejor utilizar al histograma.
Variable continua
Las variables continuas son aquellas que pueden tomar infinitos valores dentro de un rango. Dicho de otra forma, podemos describirlas con tanta precisión como queramos. Y es que la edad podemos expresarla en años, pero también podemos seguir afinando a días, minutos, segundos, poniendo tantos decimales como quisiéramos de forma indefinida.
Para poder representar datos continuos, tenemos que unirlos en intervalos, agrupando todos aquellos que caen dentro de un cierto rango de valores.
Aunque no hay una regla fija, se suelen agrupar los datos de un histograma de manera que nos caben saliendo entre 5 y 20 intervalos.

En nuestro caso, podemos conseguirlo agrupando en grupos de edad de 5 años. Por ejemplo, podemos contar el número de personas que ganaron el oro cuando tenían entre 10 y 15 años, de 15 a 20, y así sucesivamente.
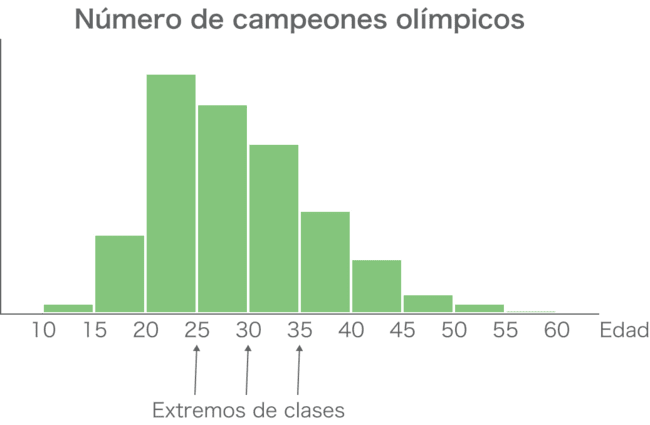
En el eje horizontal debemos indicar a qué intervalo corresponde cada barra. La forma más habitual es anotar los valores que delimitan los intervalos, a los que llamamos extremos de clase.
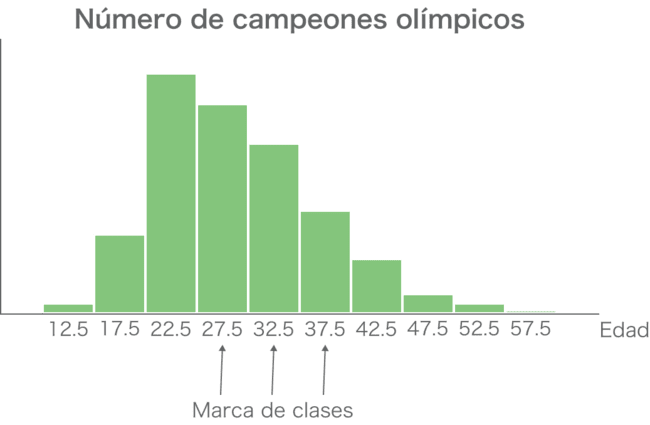
Otra es hacer la media de ambos valores y ponerla bajo cada barra. Este valor medio recibe el nombre de marca de clase de ese intervalo.
Diferencia entre histograma y diagrama de barras
Hay varias cosas en las que un histograma se diferencia de un diagrama de barras. Por ejemplo, las barras deben dibujarse pegadas unas a otras, para que se vea con claridad que estamos representando un espectro continuo de valores.
Además, en un histograma la frecuencia es proporcional a la superficie de las barras, no a su altura. Cuando los intervalos tienen el mismo ancho esto es irrelevante, porque entonces la altura también representa la frecuencia. Pero cuando los intervalos son heterogéneos es un poco más complicado.
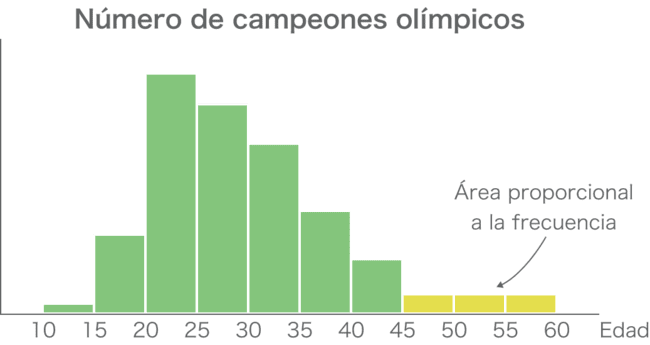
Por ejemplo, imagina que queremos agrupar los últimos intervalos en uno solo, para incluir a todos los campeones de 45 años o más. Ahora el último intervalo es más ancho que los demás, así que hay que asignarle una altura menor, de tal manera que su área siga siendo proporcional a su frecuencia. Date cuenta de lo interesante que es esto. En los diagramas de barras la clave es la altura de las barras, sin embargo en los histogramas lo que importa es el área de cada una de ellas. Los histogramas se usan para representar todo tipo de datos continuos.

Por ejemplo, en fotografía el histograma se utiliza para analizar el balance de tonos claros y oscuros de una imagen, un buen ejemplo de cómo las herramientas estadísticas pueden aportar valor en los lugares más insospechados.
Y es que efectivamente mucho ha cambiado desde los tiempos en los que nuestro misterioso medallista fue fotografiado antes de desaparecer.
Conclusiones
- Los histogramas se usan para representar todo tipo de datos continuos.
- Las variables continuas pueden tomar infinitos valores dentro de un rango.
- Para poder representar datos continuos, tenemos que unirlos en intervalos.
- Se recomienda agrupar los datos entre 5 y 20 intervalos para tener un correcto histograma,
- Las barras de los histogramas van pegadas a diferencia de los gráficos de barra que van separadas.
- Un histograma la frecuencia es proporcional a la superficie de las barras, no a su altura.


